Networking Theories to Design Techtivities to Promote Students’ Covariational Reasoning
Heather Lynn Johnson, University of Colorado Denver, USA
Consider a situation involving a cart on a turning Ferris wheel. Focus on two attributes of the situation: The cart’s height from the ground (vertical distance), and the cart’s width from the center (horizontal distance). For a single revolution of a Ferris wheel, conceive of how one could measure width and height, how width and height could vary, and how one might form a relationship between width and height. At its essence, covariational reasoning entails conceiving of a relationship between attributes that are capable of varying and possible to measure. It is imperative for students to have opportunities to develop and employ covariational reasoning. Yet, many students lack such opportunities. Building from the work of mathematics education researchers, I led the development of a suite of Techtivities—free, accessible, digital media activities linking dynamic animations and graphs. Using a Ferris wheel Techtivity to illustrate (Figure 1), I share four key design components and three theoretically based design principles grounding the Techtivities. The design components and principles emerged from networking theories of different grain sizes, namely Thompson’s theory of quantitative reasoning and Marton’s variation theory. Networking these theories informed design both across and within the Techtivities. To provide evidence for the utility of these Techtivities in promoting students’ covariational reasoning, I share student data. I discuss implications stemming from students’ opportunities to use free, accessible, digital media activities, such as Techtivities, to promote their covariational reasoning.
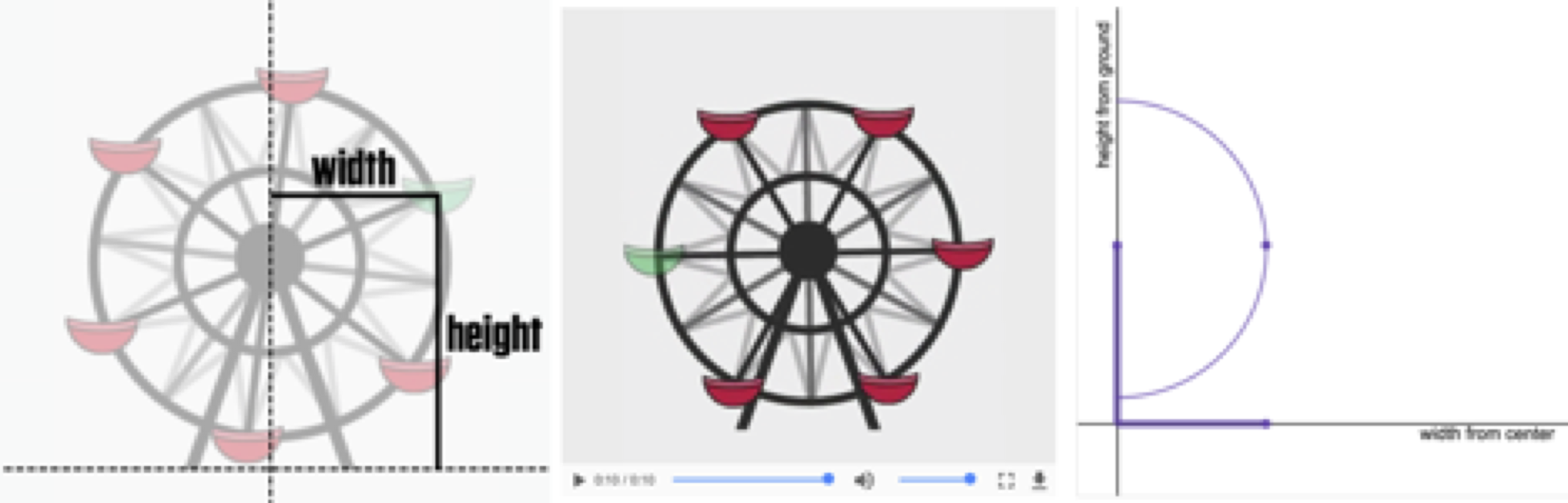
Figure 1. A Ferris wheel Techtivity.
Johnson, H. L. (2017, November). Networking theories to design techtivities to promote students’ covariational reasoning. Universiteit Utrecht Freudenthal Institute Research Meeting. Utrecht, Netherlands.